2020年1月23日,武汉封城。有研究此前认为,这一人类史上最大的隔离事件,让中国新冠肺炎感染者减少了七十多万人,对疫情的遏制起到了至关重要的作用,为全国乃至全球赢得了宝贵的时间。那么武汉封城及停学、停工等隔离措施对武汉本身的疫情防控起到了什么作用?封城又应该在何时取消?
国际顶级学术期刊《柳叶刀-全球健康》当地时间3月25日发表的一项研究,通过数学建模的方式回答了上述两个问题。该研究显示,停学、停工等增加人与人之间物理距离的干预措施,极大地减少了武汉新冠感染患者数,并推迟了流行病高峰的出现。而相比3月份解封,4月份解封更为合适。
值得注意的是,这一分析结果也与武汉实际解封计划一致。根据安排,从4月8日零时起,武汉市将解除离汉离鄂通道管控措施,有序恢复对外交通。
以上研究来自全球顶尖的医学院之一伦敦卫生与热带医学院,通讯作者为该学院传染病流行病学系传染病数学建模中心的负责人Kiesha Prem博士。
研究提示了推迟解封的重要性。数学模型的预测表明:1100万人口的武汉如果在4月初开始分批复工,则此前增加人与人之间物理距离的干预措施将取得最佳效果。同时,假设4月解封,则截至2020年年中和2020年年底,感染中位数将分别减少92%(IQR 66-97)和24%(IQR 13-90)。
4月解封可以将可能出现的第二次流行病高峰往后推迟2个月,并压扁病毒流行曲线,从而可以为医疗系统提供更多的时间,以应对可能卷土重来的病毒。
值得注意的是,对于可能出现的二次高峰,此前3月25日的中欧抗疫视频会上,钟南山院士即表示:在全球疫情的背景下,为防止第二波高峰,仍应保持现有的防控措施,同时严格外防输入。当然,据央视新闻3月27日消息,他在接受央视记者采访时同样表示,“我估计国内疫情不会出现第二波高峰。在中国群防群控的基础上,新增病例可能就局限在很小的人群中。我不相信在我们这么强有力的措施下,会出现大的暴发。”
上述研究对全球200多个已经出现新冠病毒的国家和地区有借鉴意义。武汉的新冠疫情已经基本平息,目前疫情的“震中”在美国、意大利、西班牙、英国等欧美国家。论文作者表示,希望通过评估武汉的疾控干预措施对新冠疫情进展的影响,为世界其他地区提供一些新的防控思路。
据美国约翰斯·霍普金斯大学实时统计数据显示,截至北京时间30日2时39分,全球新冠肺炎确诊病例已突破71万例,达710918例,死亡病例达33551例。数据显示,全球新冠肺炎确诊病例最多的国家是美国,累计突破13万例,达135499例;死亡病例最多的国家是意大利,累计达10779例。
长期关注流行病的比尔·盖茨也认为封锁措施对控制疫情是行之有效的。当地时间3月26日,盖茨以视频连线的方式参加了CNN《全球市政厅》节目的录制。34分钟的采访,比尔·盖茨6次提到中国,强调美国需要借鉴并严格遵循中国曾经实施的封锁措施。
研究模型还表明,这些增加人与人之间物理距离的策略,其效果随年龄段的不同而不同。发病率的下降在小学生和老年人中最显著,而在工作年龄的成年人中最不显著。
研究表示,减少学校和工作场所的接触对疫情控制至关重要。如果过早取消隔离限制,由于仍然有足够的易感人群,这很容易使基本传染数(R0)再次大于1,导致感染数量继续增加。研究者建议,干预措施的解除应该是缓慢的、逐步的,一方面是为了避免感染急剧反弹,另一方面是出于物流供给等实际原因。
附:
模型研究:减少社交的干预策略对中国武汉市COVID-19流行病结局的影响
摘要:
研究者建立了针对特定年龄和特定地点的传播模型,以评估在学校和工作场所关闭的不同情况下,武汉疫情暴发的发展轨迹。
研究者发现,改变接触方式可能会大大推迟武汉的流行高峰并减少新型冠状病毒感染者的数量。如果在2020年3月取消这些限制,则新增感染的第二高峰可能会在2020年8月下旬发生。如果一个月后(即2020年4月)放宽限制,这样的二次高峰可能会推迟2个月。
背景
从1月23日起,武汉市为应对疫情采取了前所未有的隔离措施,包括扩大学校和工作场所的停业时间。研究者旨在评估扩大物理距离措施对COVID-19流行病进展的影响,希望为世界其他地区提供一些见解。
研究方法
为了评估武汉“人群之间的混合”模式的改变是如何影响疫情发展的,研究者使用了特定地点的综合性接触模式,。同时在引入学校停课、工作场所停工并减少普通社区混合活动的情景下,对特定地点的综合性接触模式进行了调整。在加入矩阵和武汉暴发的流行病学参数后,研究者使用年龄结构的易感-暴露-感染-排除(SEIR)模型对武汉扩大人与人之间的物理距离措施进行评估,模拟了武汉疫情暴发的发展轨迹。研究者采用年龄结构的流行框架将来自传播模型的流行参数的最新估计值拟合到武汉本地和国际输出病例的数据,并调查了病例的年龄分布。研究者还通过允许人们分阶段重返工作来模拟解除控制措施的过程,并研究了(3月或4月初)重返工作的影响。
发现
研究者的预测表明:如果在4月初开始交错复工,则此前的增加人与人之间的物理距离措施将取得最佳效果。此措施能将2020年年中和2020年年底的感染中位数减少92%(IQR 66-97)和24%(IQR 13-90)。将这些措施维持到4月是有好处的,因为这可以推迟和减少高峰期的高度,减少2020年底的中位流行病规模,并为医疗系统提供更多的时间来扩充和应对。然而,研究者对这种加大人与人之间物理距离措施的效果模拟,还会因新冠感染者传染性的持续时间以及小学生在流行病中的作用而发生改变。
解释
如果将武汉的隔离限制持续到4月初,则有助于推迟新冠疫情的高峰。研究者的预测表明,过早和突然取消这些干预措施,可能会导致更早的疫情次高峰。逐渐放松干预措施可以平缓疫情的次高峰。但是,研究者的分析存在局限性,其中包括R0估计值和传染性持续时间周围的较大不确定性。
介绍
2019年12月,湖北武汉暴发了新冠疫情。此后,国家和地方层面采取了前所未有的措施应对疫情。2020年1月23日,武汉执行出行禁令,所有人未经授权不得出入武汉市。随后类似的控制措施扩展到了湖北全省。
防控主要以非药物的扩大人与人间的物理距离为主,例如停课停工,同时让居民避免进入拥挤的场所,以减少疫情暴发的影响。这些措施不同于先前针对其他呼吸道传染病暴发的应对方式,极大地改变了人群中特定年龄间的混合模式。出行限制无疑减少了武汉以外地区感染,并推迟了其他地区的暴发,但混合模式的变化也影响了武汉市内暴发的轨迹。为了评估物理疏离措施对疫情的作用,研究者考察了武汉,希望为世界其他地区提供一些见解。
人与人之间的传播主要是由互动驱动,这可能因接触者的年龄和位置(即学校,工作,家庭和社区)而异。在疫情大规模持续暴发的背景下,人与人之间的接触模式将大大偏离其基线状况。在武汉发生疫情后,增加物理距离的措施(包括但不限于学校和工作场所关闭以及鼓励公众避免拥挤场所的健康促进措施)旨在彻底改变社交混合模式。
加入这些矩阵和武汉暴发的流行病学参数的最新估值后,研究者使用年龄结构的易感-暴露-感染-排除(SEIR)模型模拟了武汉在进行了物理疏离措施后(一系列包括关闭工作场所、减少普通社区中的人群汇聚)的疾病暴发持续轨迹。
方法
SEIR模型
研究者使用确定的阶段结构SEIR模型模拟了武汉疫情暴发1年内的轨迹。
研究者根据感染状况将人群分为易感性(S),暴露性(E),感染性(I)和排除(R)个体,并根据年龄分为5年范围,直至70岁,外加一个年龄段75岁及以上,总共分出16个年龄组。易感人群在接触传染性患者后,会以一个相对固定的速率被感染,随后康复或死亡。在整个传染病流行过程中,研究者假设武汉是一个封闭的系统,人口恒定为1100万(即S + E + I + R = 1100万)。研究者使用了图中所示的SEIR模型。
假定人群中有一定数量的感染者,年龄组i中特定年龄人群的混合模式改变了他们暴露于病毒的可能性。此外,研究者纳入了无症状和亚临床者的影响。尽管有证据表明他们很可能会传播此类病毒,但在撰写本文时仍无法确定这些人是否能够传播感染。研究者还考虑了一种情况,在这种情况下,研究者认为年少者相对年长的个体而言,其症状更容易是无症状(或亚临床的)且传染性较低。
对于给定的年龄段i,可以通过以下公式描述流行病转变:
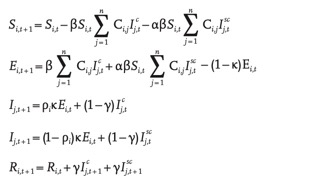
其中β是传播率(按照R0取值),Cij描述了:“年龄段j”的接触者“年龄段i”,κ= 1-exp(–1 / dL)是每日暴露的概率个体具有传染性(d为平均潜伏期),并且γ= 1–exp(–1 / dI)是当平均感染持续时间为dI时被感染个体恢复的每日概率。研究者还纳入了无症状和亚临床病例的贡献,1-ρi表示感染病例无症状或亚临床的可能性。研究者假设年轻的个体更有可能是无症状的(或亚临床的)和传染性较小的(与Ic,α相比,传染性的比例)。
使用表中提供的文献中的参数,研究者模拟了疫情。
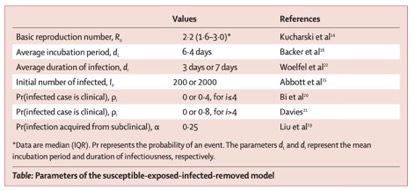
研究者假设平均潜伏期为6.4天,平均感染期为3天或7天。每次模拟都从200或2000个传染性个体开始,其余人口处于易感状态。研究者通过Kucharski及其同事从半机械模型的R0分布的后部均匀地从R0分布的95%CI得出R0值,从而探索了模型的不确定性。
社会融合和干预
社会融合模式在各个地点(包括家庭,工作场所,学校和其他位置)有所不同。在正常情况下,在所有这些地点进行的人与人之间的接触会汇总出一个总的混合方式。因此研究者对不同地点的接触模式进行了汇总,以得出暴发前总体中的基线接触模式。在暴发流行的环境中,不同的干预策略旨在减少不同情景下的社会融合,以降低病毒在人群中的传播。为了模拟旨在减少社交融合的干预措施的效果,研究者使用这些基本模式为每种干预方案创建了综合接触矩阵。
研究者考虑了以下三种情况:
第一种是理论性的情况:假设所有地点类型的社交融合方式都没有变化,学校没有寒假,没有农历新年假期;
第二种情况,没有干预措施:在有寒假和农历新年的情况下,但并未施加物理疏离措施。由于1月15日至2月10日学校放寒假,学校里没有人与人之间的接触。分别在2020年1月25日至2020年1月31日以及2020年2月1日至2月10日的期间中工作的劳动力分别为正常情况下的10%和75%;
第三种情况下,武汉采取了严厉的措施以控制疫情:假设在控制措施期间,学校停课,约有10%的劳动力(例如,卫生保健人员,警察和其他基本政府工作人员)继续工作。
对于第三种情况,研究者模拟了严格控制措施在3月或4月初结束的不同效果,并允许在学校关闭期间分阶段重返工作(即25%劳动力在第一周和第二周工作;第三,四周工作的劳动力恢复到50%;此后100%劳动力恢复工作和上学。
结果
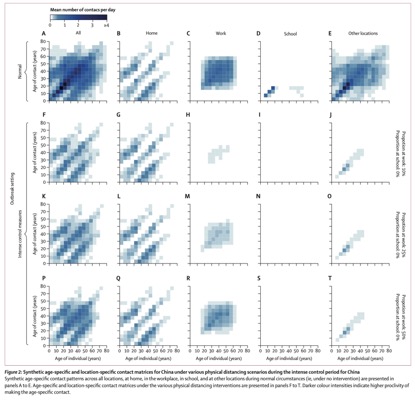
研究者的模拟结果表明,旨在减少社会融合的控制措施可以有效降低新冠疫情暴发的规模并延缓其高峰。
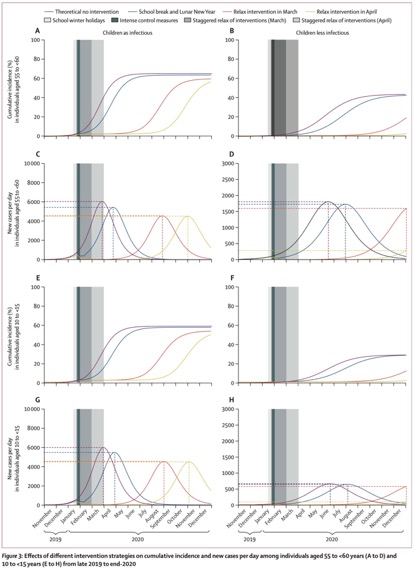
研究者提供了200次模拟暴发的中位数累积发病率,每天的新报告病例和每天的特定年龄发病率。
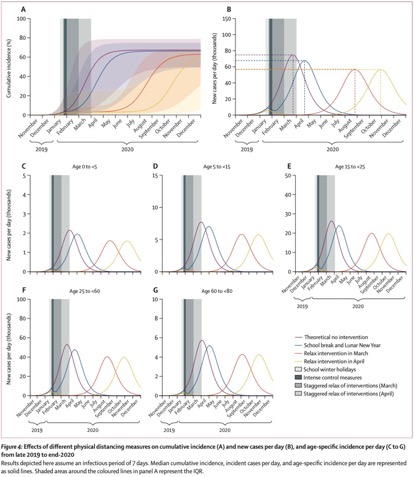
严格的控制措施,如长期停课和放假,可减少到2020年底的累计感染率和发病率高峰,同时也推迟了疫情的暴发高峰。研究者的模型表明,这些增加物理距离的策略效果随年龄段的不同而不同。发病率的下降在小学生和老年人中最显著,而在工作年龄的成年人中最不显著。
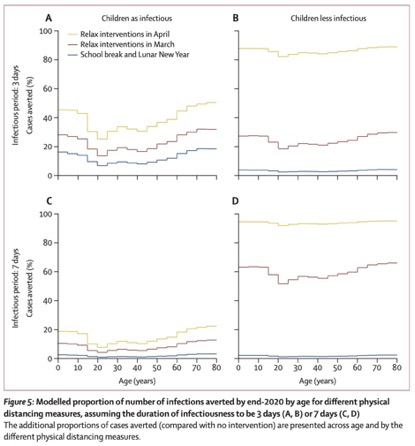
如果湖北武汉在4月初开始分批恢复工作,则最能保住此前增加物理距离的成果。由于该疾病具有更长的传染期,实行强力的隔离措施并在4月开始逐步解封,建模得出的感染的中位数到2020年中期能减少92%(IQR 66-97),到2020年底可减少24%(IQR 13-90),并降低了所有年龄段的人群发病率和发病高峰。这对减轻疫情暴发对医疗保健系统的压力有着重要的意义。 另外,R0值的不确定性对流行高峰的时间安排和暴发的最终规模有很大影响。
长时间停课和放假的严格控制措施的模拟效果随感染时间的长短而异。如果该疾病的感染期较短(3天),则研究者的模型表明,3月份放松干预措施可以避免约30%的学龄儿童和年长个体患病。如果该病具有更长的传染性持续时间(例如7天),那么3月放松将对到2020年底降低感染病例帮助不大。相比3月就解封,4月解封效果更好。在儿童传染性较低的假设下,在4月而不是3月取消物理疏远干预措施,可能会带来更多的健康益处。
讨论
数学模型可以帮助研究者了解新冠病毒如何在整个人群中传播,并为可能减轻未来传播的控制措施提供信息。研究者使用年龄结构化的SEIR模型模拟了武汉市持续暴发COVID-19的轨迹。由于个体间的混合模式并非随机,因此会影响疾病的传播动力学。评估物理疏离干预措施(例如学校停课)有效性的模型需要考虑社会结构和个体混合中的异质性。在研究者的模型中,研究者将纳入了针对特定年龄和特定地点的社会混合模式进行了改进,以估计特定地点的物理疏离干预措施在减少暴发扩散方面的效果。为减少与学校和工作场所的接触而采取的措施正在通过为医疗保健系统提供了应对的时间和机会,以便更有力的控制疫情。因此,如果过早取消隔离限制,由于仍然有足够的易感人群,这很容易使基本传染数再次大于1,导致感染数量将会增加。实际上,干预措施应缓慢、逐步取消,一方面是为了避免感染急剧增加,另一方面是出于物流供给等实际原因。因此,研究者模拟了以交错方式逐步取消干预。
研究的局限性
本研究以武汉为例,描述了一个数学模型,该模型可量化物理疏离政策的潜在影响。中国世卫组织联合考察组的流行病学调查发现,许多感染集中在家庭。这也就意味着,强力的物理疏离措施也可能带来另一些不利影响,包括学校停课,工作场所停工和避免任何公共聚会这样的措施,可能将传播推向家庭,导致家庭聚集感染案例增加。由于模型中未明确包括家庭,因此研究者没有考虑家庭传播的异质性和集群性。在接触网络模型中,区分重复接触和新接触对于疾病传播很重要;需要更复杂的方法来说明家庭中的暂时存在,以表征较高的接触程度。鉴于研究者研究的局限性,研究者的隔间模型没纳入接触者的个体水平异质性,这在超级传播事件(尤其是在流行病的早期)中可能很重要。与医院内感染相结合,确诊病例与医护人员的密切接触有可能扩大COVID-19感染的风险。但是,研究者提出的隔间模型无法明确考虑医疗机构和家庭之间的传播。
研究使用了其他研究已有的R0作为关键参数。R0决定了新冠病毒在疫情暴发初期在人群中传播的速度。但这是一个难以估计的参数。
另外,研究也未考虑天气及气候对新冠疫情的影响。也未将其他创新纳入模型,例如医院能力的提升、检测的快速扩展,这些都能缩短诊断和卫生系统的延迟,从而减少传染性和易感性个体之间的有效接触,并中断传播。正在开发的有效疫苗和抗病毒药物可以抵消这一全球公共卫生威胁。
 简体中文
简体中文